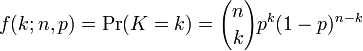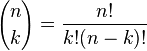bennymacca wrote:also, ill go through the maths that i used to work out the odds. (for those that aren't great with maths, skip about halfway down to where i started making estimations about jo's game)
The mathematical construct used in these situations is called a binomial distribution, which models the success of n indepentent yes/no trials, where the probability of success is p.
the probability of getting k successes in n trials, with success probability p is given by
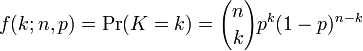
where
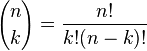
in our example, n = 5, the number of tournaments, k is the number of wins, and p is the probability of a win.
now in our case, jo's success is k >= 1 (i.e 1 or more wins). so to work out the probability, we actually work out the probability of jo not winning at all, and then take one minus that number (this way, we get the probability of 1,2,3,4, or 5 wins)
i did it by hand the first time, but then i found an
online calculator which lets you play around with the numbers easily
___________________________________________________________________________________________________________
now i will tell you how i went about calculating jo's average
first, i went through jo's results online.
since season 1 2010, he has played live 228 games, for 6 wins and 71 final tables.
this is a win percentage of 2.63% and a final table percentage of 31.14%
so now we have the parameters to plug into the binomial distribution.
n = 5, k = 1, p = 0.0263
plugging these in gives a probability of 1 or more wins as 12.48%, or odds of approximately 8:1
BUT
i figured that jo, like the rest of us when we play 888pl, doesn't take it seriously most of the time, so i estimated his win rate to be up to 3 times as high as his long term win rate because there was something on the line.
so i figured jo's win rate might actually be as high as 7%. (rightly or wrongly, this was my estimation)
if we use p = 0.07, and re-calculate the number, then we get the probability of at least 1 win P(X>=1) = 0.3043, or 3.3:1.
thus, when i was setting the odds, i decided to go slightly in my favour and set them at 2.6:1. you could argue that my estimate of jo's win rate was too high but meh.
i did the same thing with the final table percentage, but i used jo's long term final table percentage to calculate the odds of a final table, and it turns out that, jo will make a final table at least once in 5 games, 84% of the time. so thats where the 1:7 odds came in, but i was always expecting to lose that bet as i didn't take into account a higher percentage from jo playing properly.
so hopefully i have explained it ok. basically if you use the online calculator you dont need to know any of the maths and you can still work out some stuff.
if you ever want to have any more of these challenges, i am happy to give you some more action, but i guess the odds will be different this time as you will know more about what odds are realistic.
Cheers
Barb